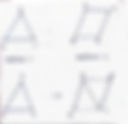Search Results

The statement is: ? - A is 6 + 3, B = 5+4, A = B. In Prolog, the expression is is used for arithmetic evaluation, while = is used for unification. So, the query you provided will result in a false statement because B is unified before arithmetic evaluation: ?- A is 6 + 3, B = 5 + 4, A = B. false. This is because A is unified with the result of arithmetic evaluation (9), while B is unified with the term "5+4", which is not equal to 9.

Rationality is nothing but status of being reasonable, sensible, and having good sense of judgment. Rationality is concerned with expected actions and results depending upon what the agent has perceived. Performing actions with the aim of obtaining useful information is an important part of rationality. Rationality of an agent depends on the following − The performance measures, which determine the degree of success. Agent’s Percept Sequence till now. The agent’s prior knowledge about the environment. The actions that the agent can carry out. A rational agent always performs right action, where the right action means the action that causes the agent to be most successful in the given percept sequence. The problem the agent solves is characterized by Performance Measure, Environment, Actuators, and Sensors (PEAS).

The statements are given as follows: P ∨ (~P & Q & R) (~P & Q) ∨ (P & ~Q) & S Conjunctive normal form implies that all terms in the equation must have the "&" symbol between them. In the two sentences given above, we can see we have the "∨" symbol between the terms. Let us convert each of them into conjunctive normal form one-by-one. Statement 1: P ∨ (~P & Q & R) P ∨ (~P & Q & R) = (P ∨ ~P) & (P ∨ Q) & (P ∨ R) = (P ∨ Q) & (P ∨ R) We used two properties here: While opening the brackets, whatever is outside the bracket must be multiplied/operated with each term inside the bracket. (P ∨ ~P) = NULL, as it is always TRUE. Statement 2: (~P & Q) ∨ (P & ~Q) & S (~P & Q) ∨ (P & ~Q) & S = ((~P ∨ (P & ~Q)) & (Q ∨ (P & ~Q))) & S = ((~P ∨ P) & (~P ∨~Q)) & ((Q ∨ P) & (Q ∨~Q)) & S = (~P ∨~Q) & (Q ∨ P) & S We have converted both statements into Conjunctive Normal Form.

Admissibility of an algorithm typically refers to whether a search algorithm is guaranteed to find an optimal solution, assuming one exists. An admissible algorithm always finds the least-cost path to the goal (the optimal solution) if such a path exists. For example, in pathfinding problems, an admissible algorithm ensures that the path found is the shortest or has the least cost among all possible paths. In the context of heuristic search algorithms, such as A* (A-star), admissibility is closely tied to the heuristic function used. For A* to be admissible, the heuristic function ℎ(𝑛) (which estimates the cost from node 𝑛 to the goal) must be optimistic, meaning it never overestimates the actual cost. In other words, it must always underestimate the cost. Formally, this is written as: ℎ(𝑛)≤ℎ∗(𝑛), where ℎ∗(𝑛) is the true cost from node 𝑛 to the goal. Admissibility is crucial in applications where finding the best possible solution is important, such as in routing, game playing (e.g., chess), and various optimization problems. Let us understand overestimation and underestimation with an example. Example of Overestimation: Let’s suppose, you are going to purchase shoes and shoes have a price of $1000. Before making the purchase, you estimated that the shoes would be worth $1200, When you went to the store, the shopkeeper informed you that the shoe’s actual price was $1000, which is less than your estimated value, indicating that you had overestimated their value by $200. so this is the case of Overestimation. 1200 > 1000, i.e., h(n) ≥ h*(n) ∴ Overestimation Example of Underestimation: Similar to the last situation, you are planning to buy a pair of shoes. This time, you estimate the shoe value to be $800. However, when you arrive at the store, the shopkeeper informs you that the shoes’ true price is $1000, which is higher than your estimate, indicating that you had underestimated their value by $200. In this situation, Underestimation has occurred. 800 < 1000, i.e., h(n) ≤ h*(n) ∴ Underestimation Now, let us understand this in a bit more detail with the help of A* Algorithm. In the graph above, X is the start node and Y is the goal node. In between these two nodes there are intermediate nodes A and, B and all values which are in the above diagram are actual cost values means h*(n). Overestimation Let’s suppose, H(A)= 60 H(B)= 50 So, using A* equation, f(n) = G(n) + h(n) by putting values f(A) = 100 + 60 = 160 f(B) = 100 + 50 = 150 by comparing f(A) & f(B), f(A) > f(B) so choose path of B node and apply A* equation again f(Y) = g(Y) + h(Y) [here h(Y) is 0, Goal state] = 140 + 0 [g(Y)=100+40=140 this is actual cost i.e. h*(B)] = 140 The least cost to get from X to Y, as shown in the mentioned graph is 130, however, in Case 1, we took into consideration the expected costs h(n) of A & B, which were 60 & 50, respectively. As a result, 140 > 130 according to the Overestimation condition h(n) ≥ h*(n), and here, since the value of node f(A) is bigger than f(Y), we are unable to proceed along a different path which is from node A. Underestimation Let’s suppose, H(A) = 20 [This are estimated values i.e. h(n)] H(B) = 10 So, using A* equation, f(n) = G(n) + h(n) by putting values f(A) = 100 + 20 = 120 f(B) = 100 + 10 = 110, by comparing f(A) & f(B), f(A) > f(B), so choose path of B node and apply A* equation again f(Y) = g(Y) + h(Y) [here h(Y) is 0, because it is goal state] = 140 + 0 [g(Y) = 100 + 40 = 140 this is actual cost i.e. h*(B)] = 140 Now, notice that f(Y) is the same in both circumstances but, in 2nd case by comparing the f(A) with f(Y) i.e. 120 < 140 as it means we can go from node A. Therefore A* will go with f(A), which has a value of 120.

The parse tree is a graphical structure that divides the sentence into its components. Each sentence is represented by S and is composed of NP (Noun Part) and VP (Verb Part). The parse tree structure of the given sentence will be as follows:

Let us start by constructing the truth table for A∨B. Now, let us extend this truth table to include A&(A∨B). As we can see that the truth column for A&(A∨B) is the same as the truth table for A. Hence, we can say that A&(A∨B) = A. In other words, the single term which this expression is equal to is A.

This question can be solved using Baye's Theorem. Baye's theorem can be stated mathematically as: P(A|B) here implies the probability of occurrence of event A, given event B has already occurred. We know that P(B|A) = 0.84 P(A) = 0.2 P(B) = 0.34 Inputting this in the equation, we get, Solving this, we get 0.49. This is our required answer.

A recursive transition network (RTN) is a graph schematic that represents the rules of Context Free Grammar (CFG). We can see that the given sentence is "The Silly Robot moved the Red Box to the Red Table". Let us write a context-free grammar from this. We know that all context-free grammars start with S, which implies "sentence". The sentence has two parts - Noun Part and Verb Part. S 🡢 NP | VP The Noun Part can be either a Determinant, Adjective or Noun. NP 🡢 DET | ADJ | N The Verb Part can either be a Verb, Noun Part or Preposition Part. VP 🡢 V | NP | PP DET can be the. DET 🡢 the Similarly, ADJ can be silly or red. ADJ 🡢 silly | red Noun can be robot, box or table. N 🡢 robot | box | table Verb can be moved. V 🡢 moved Preposition Part can be Preposition or Noun Part. PP 🡢 PREP | NP And finally, preposition can be to. PREP 🡢 to Let's write all these rules together. S 🡢 NP | VP NP 🡢 DET | ADJ | N VP 🡢 V | NP | PP PP 🡢 PREP | NP DET 🡢 the ADJ 🡢 silly | red N 🡢 robot | box | table V 🡢 moved PREP 🡢 to Now that we have our CFG, we can use it to draw RTN. RTN is same as CFG, except for the fact that it uses graphical diagrams. The following will be the RTN of this CFG:

We can represent the comparisons made along a root-to-leaf path in the decision tree as a directed graph. Each node represents an element of the array 𝐴[𝑖]A[I]. An edge from node 𝑖 to node 𝑗 indicates a comparison between 𝐴[𝑖]A[i] and 𝐴[𝑗]A[j]. For the permutation at a leaf to be correctly determined, the comparison graph must be connected. This means there must be a path of comparisons connecting every pair of nodes. If the graph is not connected, there will be at least two disjoint subsets of elements whose relative order hasn't been determined. In an undirected graph, a tree with 𝑛 nodes has 𝑛−1 edges and is connected. Similarly, in a directed graph representing comparisons, you need at least 𝑛− comparisons to ensure connectivity. Therefore, with fewer than 𝑛−1 comparisons, you cannot guarantee that the graph is connected, meaning there would be some relative orders of elements that are not determined. Hence, the smallest possible depth of a leaf in a decision tree, where the permutation of elements at that leaf is guaranteed to be correct, is indeed 𝑛−1. This means that in the best case, you would need at least 𝑛−1 comparisons to fully determine the correct order of 𝑛 elements. This depth would correspond to a scenario where the algorithm encounters a highly favorable input sequence, such as an already sorted array in some comparison sorts (e.g., insertion sort). However, this is not the average or worst-case depth, which for comparison-based sorting algorithms is generally 𝑂(𝑛log⁡𝑛).

Before we proceed, make sure you know what the Fibonacci Series is. The Fibonacci sequence is a type series where each number is the sum of the two that precede it. It starts from 0 and 1 usually. The Fibonacci sequence is given by 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on. The numbers in the Fibonacci sequence are also called Fibonacci numbers. The nth Fibonacci number is calculated by adding thee (n-1)th and (n-2)th number of the Fibonacci Series. Let's write a function called "fib" that takes in two parameters - n: The position in the Fibonacci sequence for which we want to find the value. memo: An object used to store previously computed Fibonacci values to avoid redundant calculations. function fib(n, memo) {    memo = memo || {}    if (memo[n]) {       return memo[n]    }    if (n <= 1) {       return 1    }    return memo[n] = fib(n - 1, memo) + fib(n - 2, memo) } Let us see what each line of the function implies: memo = memo || {}: If memo is not provided (or is undefined or null), it initializes memo as an empty object. This ensures that memo is always a valid object. if (memo[n]) { return memo[n] }: This line checks if the Fibonacci number for the given n has already been computed and stored in memo. If it exists (memo[n] is truthy), the function returns this precomputed value, avoiding further computation. if (n <= 1) { return 1 }: This handles the base cases of the Fibonacci sequence. By definition, fib(0)=1fib(0)=1 and fib(1)=1fib(1)=1. The function returns 1 when n is 0 or 1. return memo[n] = fib(n - 1, memo) + fib(n - 2, memo): If the value for n is not already in memo and n is greater than 1, the function computes it recursively. The result is the sum of the Fibonacci numbers for n - 1 and n - 2. This computed value is then stored in memo[n] before being returned. Storing the value ensures that future calls to fib with the same n can return the precomputed result, thus reducing the time complexity. The best case time complexity of this is O(1), while the worst case is O(n).

The question at hand is: The BFS algorithm has been used to produce the shortest paths from a node s to all other nodes in a graph G. Can Dijkstra's algorithm be used in place of BFS? In a different scenario. Dijkstra's algorithm has been used to produce the shortest paths from a node s to all other nodes in a graph G'. Can BFS be used in place of the Dijkstra's algorithm? Explain your answers for both scenarios. Before we answer this question, you should know what BFS Algorithm and Dijkstra's Algorithm is. If you do not know what these algorithms are, I suggest that you read my article on these algorithms. We know that Dijkstra's Algorithm is applied on a weighted graph. If we try applying Breadth First Search on such a graph, the algorithm fails. Hence, we cannot use BFS in place of Dijkstra's Algorithm. However, when it comes to unweighted graphs, the situation is different. We know that usually BFS is applied to unweighted graphs only. When we replace this algorithm with Dijkstra's Algorithm, no major effect takes place because unweighted graph is just a weighted graph with all weights as ZERO or NULL. Hence, Dijksta's Algorithm CAN be used in place of BFS Algorithm. However, BFS Algorithm cannot be used in place of Dijksta's Algorithm.

The given question is: Given two keyframes for an object transformation, the first keyframe contains a triangle and the second keyframe contains a quadrilateral. Convert the triangle into the quadrilateral by equalizing vertex counts. Let us answer this question step-by-step. First of all, let us see what keyframes are. Keyframes are specific frames in an animation timeline where the animator sets the critical positions, poses, or states of an object. They serve as the main checkpoints that define the motion or transformation of the animated subject. The purpose of keyframes is to establish the primary structure of the animation. They provide a framework for the software to interpolate the in-between frames, creating a smooth transition from one keyframe to another. Now, we have been given two keyframes - one of a triangle and the other of a quadrilateral. The two keyframes can be drawn as follows: Now, we know that a triangle has three vertices and a square has four vertices. To equalize both the keyframes, they must have the same number of vertices. Hence, we must add one more vertex to the triangle to equalize the keyframes. As we can see that we have successfully converted the triangle to a quadrilateral by equalizing vertex counts.