This is the official question paper of Computer Graphics Paper of B.Sc. (Hons.) Computer Science Course at the University of Delhi.
Question 1 to 7 are compulsory.
Attempt any four questions from question 8 to question 14.
Part of a question must be answered together.
Some symbols may not be visible on mobile devices. Hence we recommend that you use a desktop to view the solutions to the questions.
Question 1 (a): What is a Polygon Mesh? List any one polygon mesh representation.
Question 1 (b): Consider a polygon with vertices ABCD with coordinates A(1,2), B(6,6), C(8,3) and D(5,10). Trace the contents of the Active Edge Table according to scan line fill algorithm.
Question 2 (a): Define horizontal and vertical retracing.
Question 2 (b): What are the properties of unweighted area sampling technique of anti-aliasing?
Question 3 (a): Why is depth-sort algorithm for visible surface determination called painter’s algorithm?
Question 3 (b): Prove that parallel lines remain parallel under 2-D Transformations.
Question 4 (a): Differentiate between orthographic and oblique projections.
Question 4 (b): Rotate a triangle with coordinates A(0,0), B(1,1), C(5,2) by 45° about coordinate C in clockwise direction.
Question 5 (a): How to convert RGB color model to CMY color model?
Question 5 (b): Draw a 3 × 3 pixel grid pattern to display 10 intensities on a bi-level system display. Show patterns for all the intensity values.
Question 6 (a): What is the condition to switch from region 1 to region 2 of the first quadrant of an ellipse in mid point ellipse drawing algorithm?
Question 6 (b): What is diffuse reflection? How is it different from specular reflection?
View Solution
Question 7 (a): Differentiate between cabinet and cavalier parallel projections.
Question 7 (b): Write the 4×4 3-D transformation matrices for each of the following transformations respectively :
(a) Uniform scaling to double the size of an object.
(b) Translate an object 2 units in x direction and 3 units in y direction.
Question 8 (a): Explain briefly raster scan display architecture.
View Solution
Question 8 (b): Give the steps to clip the lines PQ and RS (having coordinates P(5,12), Q(20,25), R(11, 8) and S(25,16)) against the clip rectangle ABCD (having co-ordinates A(10,20), B(20,20), C(10,0), D(20,10)) using Cohen Sutherland Line Clipping Algorithm.
View Solution
Question 9 (a): Consider a 3D object with coordinate points P(0,3,3), Q(3,3,6), R(3,0,1) and S(0,0,0). Perform a local scaling on the object with scaling factors of 2, 3 and 3 along X, Y and Z axes respectively, to obtain the new coordinates of the transformed object.
View Solution
Question 9 (b): A cubic Bezier curve segment is described by control points P0(2,2), P1(4,8), P2(8,8) and P3(9,5). Another curve segment is described by Q0(a,b), Q1(c,2), Q2(15,2) and Q3(18,2). Find the values of a, b, and 10. (ac such that the curve segments join smoothly and C1 continuity exists between them.
Question 10 (a): Write steps to shade an object using Phong shading method of polygon rendering? How does it overcome the drawback of Gouraud shading method?
Question 10 (b): Consider a line from (0,0) to (5,5). Rasterize the line using Bresenham's line drawing algorithm.
Question 11 (a): Reflect the polygon whose vertices are A(-1,0), B(0, -2), C(1,0) and D(0,2) about the line x =2 using homogeneous co-ordinates.
Question 11 (b): Clip the polygon ABCD with the vertices A(7,0), B(5,12), C(7,7) and D(6,2) against the window P (2,0), Q(10,0), R(10,10) and S(2,10) using the Sutherland-Hodgeman Polygon Clipping algorithm. Also show output vertex array at each step.
Question 12 (a): Explain Hue, Saturation and Value in HSV color model.
Question 12 (b): Consider a line segment AB parallel to the Z axis with end points A[3 2 2 1] and B[3 2 4 1]. Overall scale to double the size of line AB followed by two point perspective projection with COP along X-axis and Y-axis as Xc=10 and Yc=20 respectively. Also, write the corresponding vanishing points.
Question 13 (a): Explain depth sort algorithm for visible surface determination.
Question 13 (b): A rectangular parallelopiped is given. Its length on x-axis. y-axis and z-axis is 3, 2 and 1 respectively. Perform a rotation by an angle 90° about x axis followed by a rotation by an angle 90° about y axis.
View Solution
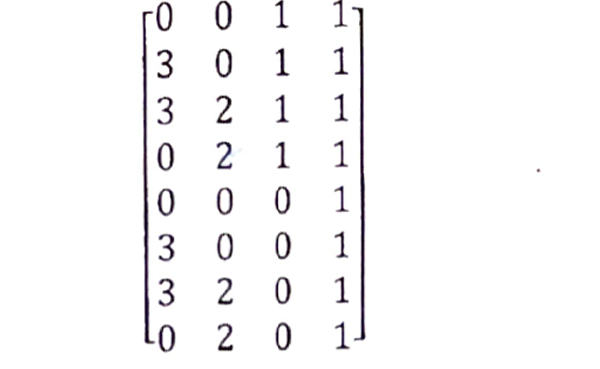
Question 14 (a): Consider a rectangular parallelepiped with the given coordinates:
Apply a trimetric projection on the given position vectors by an angle of Φ=30° about the y-axis, followed by a rotation by angle θ=45° about the x-axis, followed orthographic parallel projection onto the z=0 plane. Also, find the three foreshortening ratios.
View Solution
Question 14 (b): Given two keyframes for an object transformation. The first keyframe contains a triangle and the second keyframe contains a quadrilateral. Convert the triangle into the quadrilateral by equalizing vertex counts.
END OF PAPER