Let G = (V,E) be a directed unweighted graph. Given two vertices s and t in V, what is the time required to determine if there exists at least one s-t path in G? Can we use the DFS algorithm to fin...

The given question is:

"Let G = (V,E) be a directed unweighted graph. Given two vertices s and t in V, what is the time required to determine if there exists at least one s-t path in G? Can we use the DFS algorithm to find the shortest-path distance from the s to t? If yes, justify, otherwise give a counter-example."

Either Breadth First Search (BFS) or Depth First Search (DFS) can be used to find path between two vertices. Take the first vertex as a source in BFS (or DFS), follow the standard BFS (or DFS). If the second vertex is found in our traversal, then return true else return false.

The time complexity of this algorithm is O(V+E), where V is the number of vertices and e is the number of edges. Breadth-First search can be useful to find the shortest path between nodes, and depth-first search may traverse one adjacent node very deeply before ever going into immediate neighbours. DFS may or may not find the shortest path from s to t.

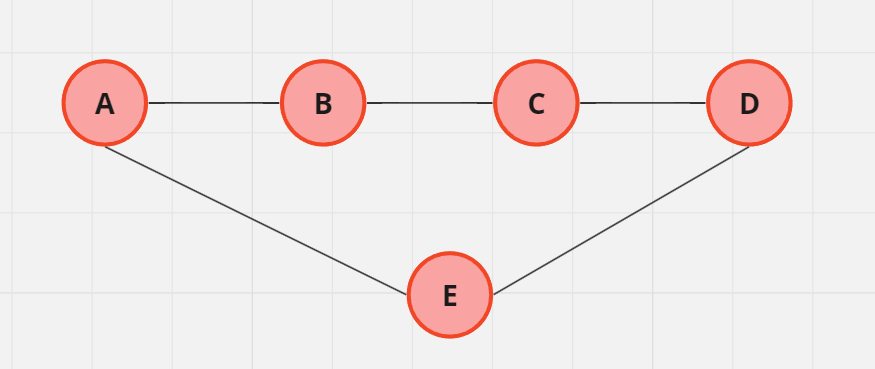
An example of this is shown below:

Here, we have to find a path from A to D. Now, we know that the shortest path is A→E→D. However, Depth First Search might start exploring A→B→C→D path first and it will return this path, which is not the shortest path between A and D.